<% String state = request.getParameter("state");
if (state == null)
state = "0"; %>
|
Radiation exchange determines the thermal regime of a snow cover.
Thermal conduction in snow is limited by the amount contact
between ice particles. A newly fallen dry snow offers less of contact
between ice particles and hence is an efficient insolating material. In
contrast, a dense and wet spring-snow is an efficient T-conductor.
|
| |
| Material |
k
: thermal conductivity coefficient |
| Air |
0.022 |
| Snow |
0.040 |
| Mineral Wool (Building
Insul.) |
0.042 |
| Water |
0.580 |
| Ice |
2.210 |
|
|
Formula 1. :
| Heat
flux through snow |
| q
= k x dT/dx |
|
|
|
q [W/m2]
k [W/(m°K)] thermal conductivity coefficient
T [°K] Temperature in Kelvin
x [m] distance over which heat flow is calculated
|
|
The thermal conductivity coefficient k
increases markedly with increasing snow density, as the number of ice
particles in contact increases per volume of snow.
|
 |
 |
|
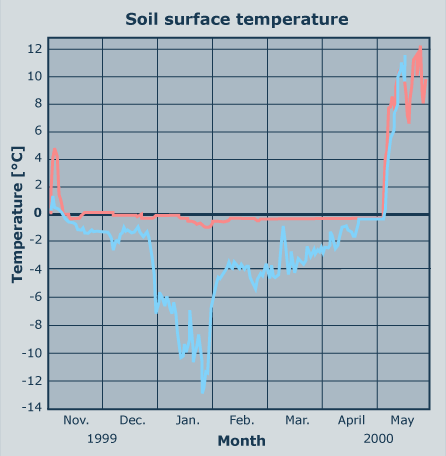
Here you see the soil surface temperature graphs from two
neighbouring locations. Observe the temperature differences and decide
which graph shows the conditions on the location with the thicker snow
cover.
|
|
Help?
|
 |
|
1 - Development of the soil surface temperature of an alpine
meadow near Nendaz (2125m), Switzerland, and of an alpine meadow sparsely
covered with snow near Zermatt (2300m) between November 1 1999 and May
29 2001, Switzerland
|
2 - Example of the snow cover in a wind-rich area with low
snow depth. (128K)
|
|
| |

